NIGHT MODE
DAY MODE


data golf Live Model
EUR ISPS HANDA - CHAMPIONSHIP
Live finish probabilities, updating every 5 minutes.
MORE LIVE MODELS...
LIV Adelaide
KFT Veritex Bank Championship
DFS SHOWDOWN PROJECTIONS...
UPDATE FEED — VIEW ALL
RANKINGS
ARCHIVES
Raw Scores, Stats, and Strokes Gained
Betting Odds
DFS Points & Salaries
Betting Results
INTERACTIVES
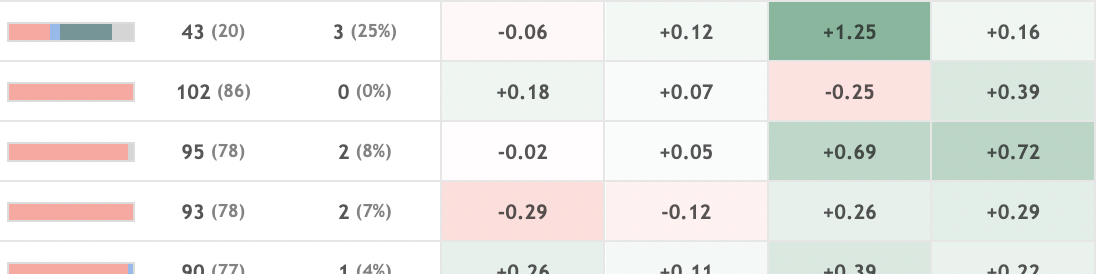
Trend Table 



Interactive table highlighting recent performance trends around the world of golf.
Approach Skill
Using strokes-gained, proximity, and GIR to break down approach skill across 6 yardage buckets.


Historical EventTournament Stats
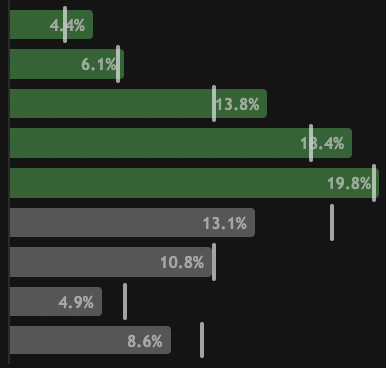
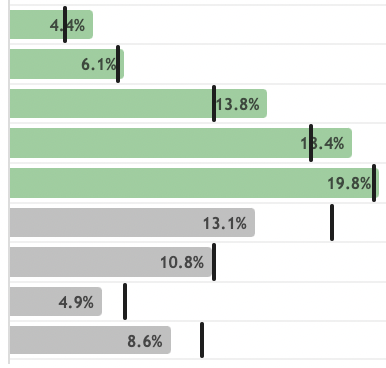
Comprehensive statistical breakdown of past PGA Tour tournaments.
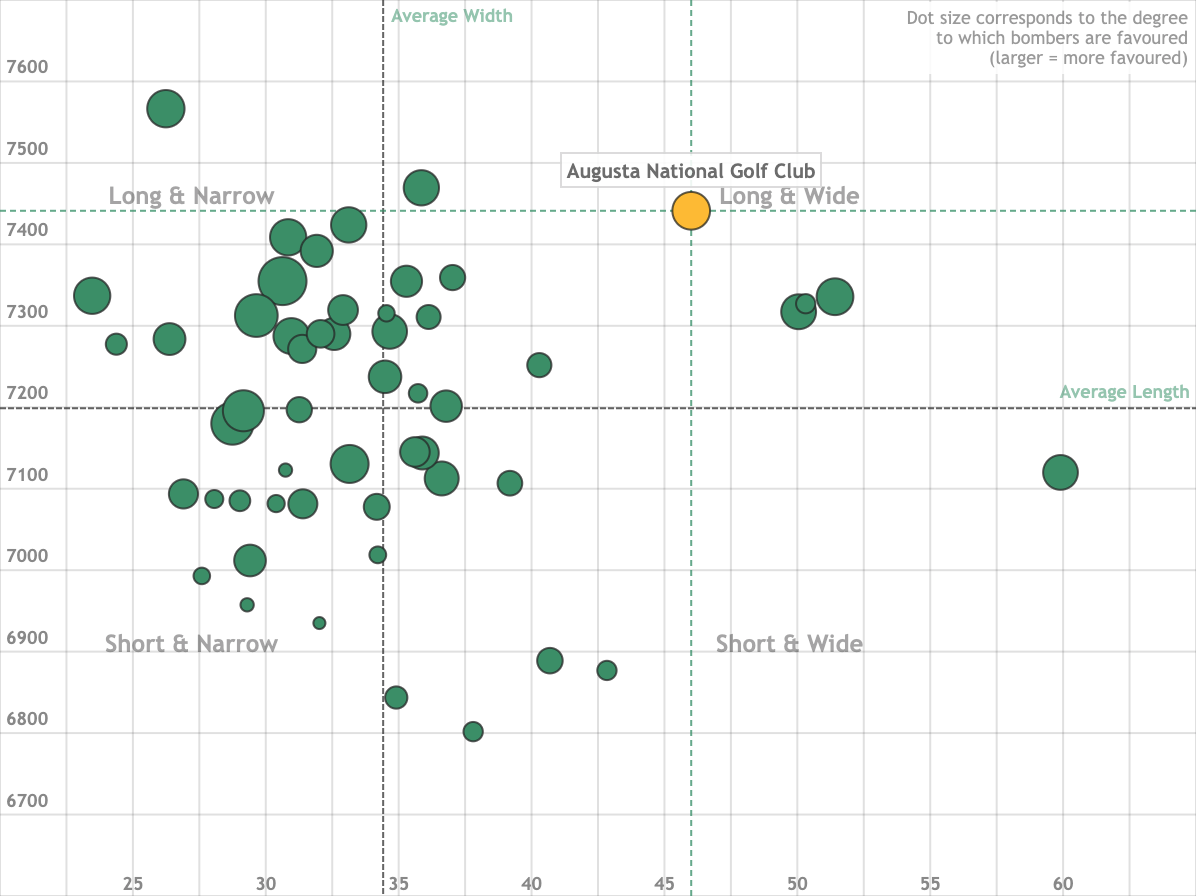
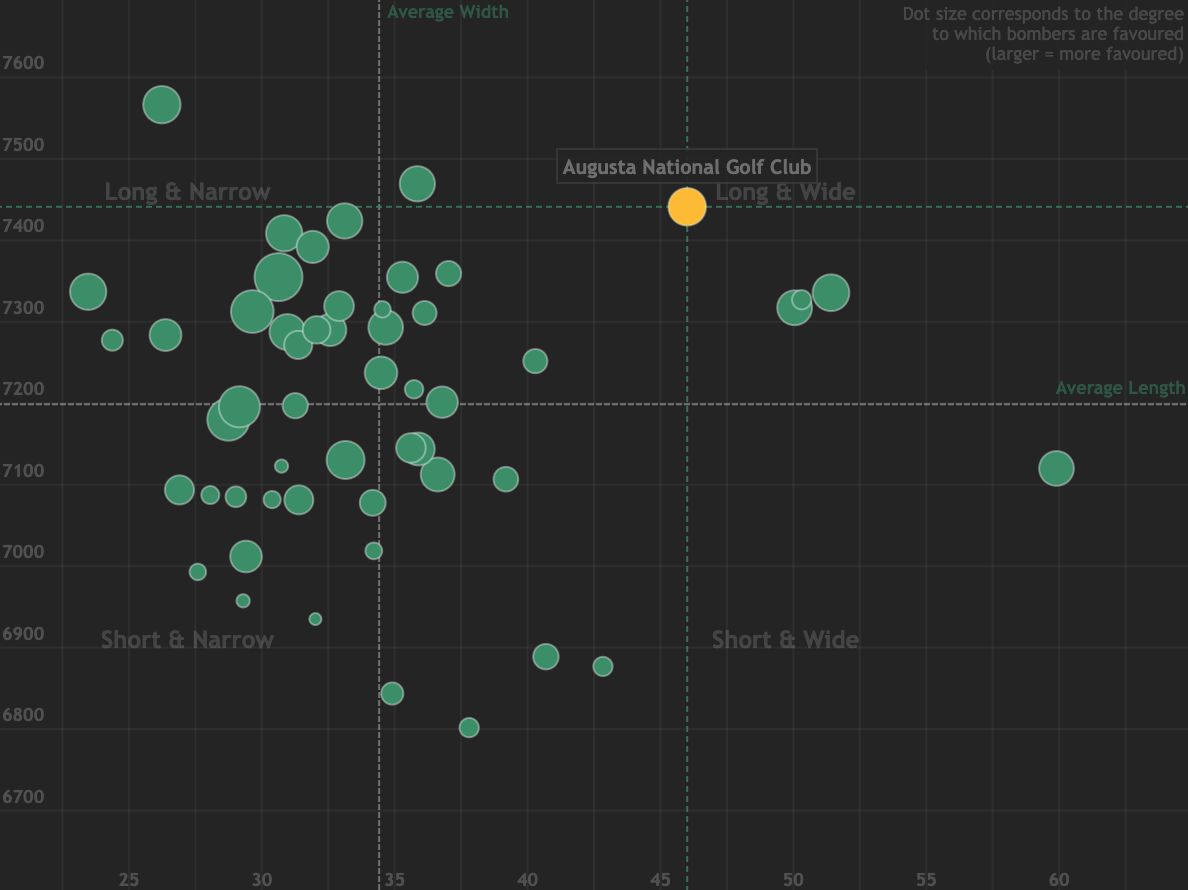
Course Fit Tool
Are certain skill sets — such as distance, or accuracy — favoured at specific courses?

SGStrokes-Gained Distributions
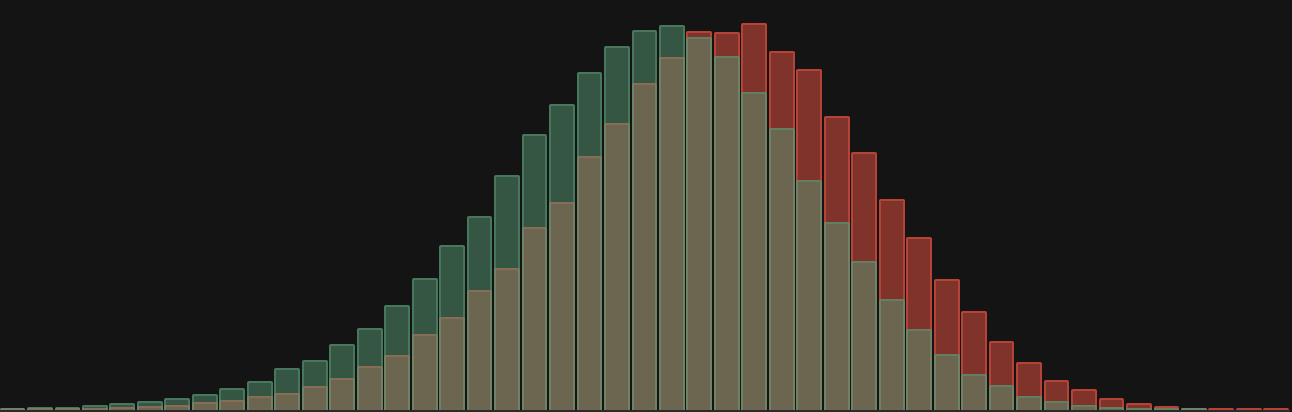
Ranking and visualizing the round-level distribution of strokes-gained.
Performance Table
Pressure Tool
Who plays best (and worst!) under pressure?
Career Projections

Letzig's Latest
Our weekly newsletter, delivered to your inbox every Wednesday morning.
Read the latest issue.
Tournament Summaries


Summarizing tournaments by their distribution of skill, difficulty to win, and entertainment value.
Bet Tracker
API Access
PLAYER PROFILES

 HOJGAARD NICOLAI
HOJGAARD NICOLAI
DG RANK
80th
OWGR RANK
35th
data golf
scratch tools
Full-field win and top 5/10/20 predictions from our model listed alongside odds from various books.
View our model's odds and track line movement for matchups and 3-balls offered at popular books.
Model odds for common 'prop' bets such as winning margin and winner's nationality, as well as a custom group simulator.
Use our model to simulate matchups and 3-balls between any golfers from our database.
MODEL PREDICTIONS
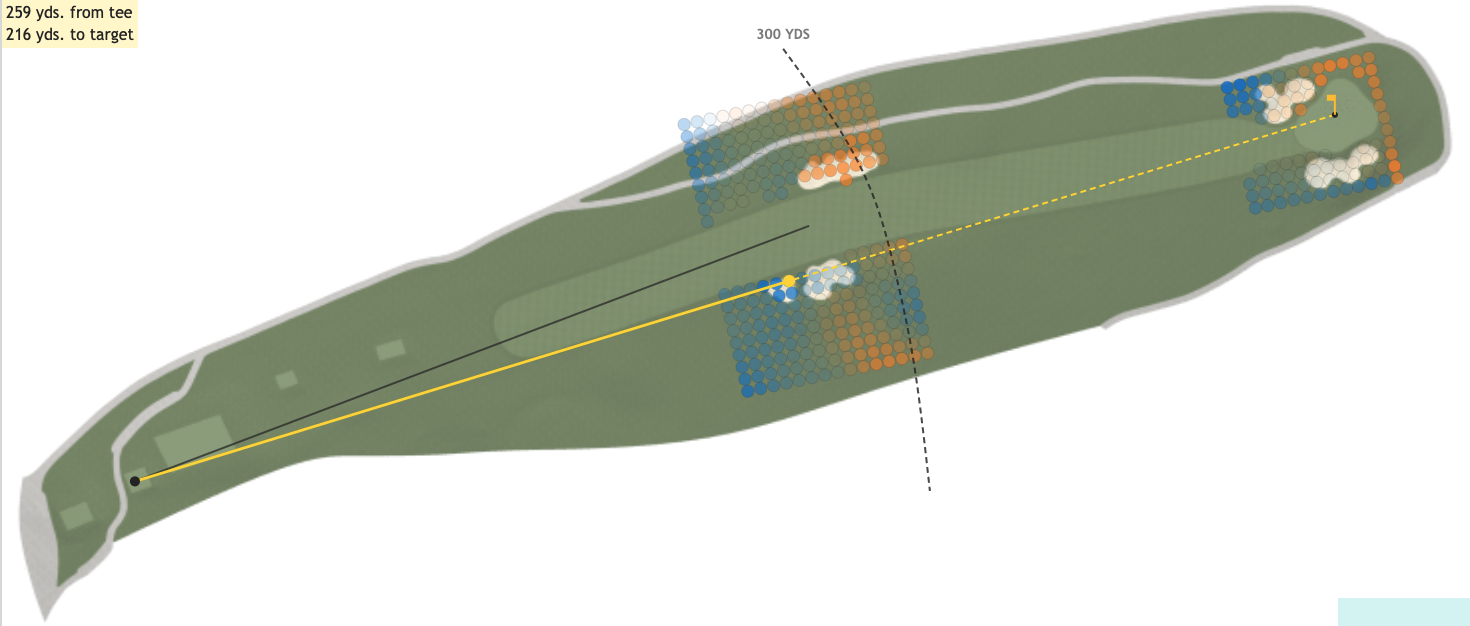
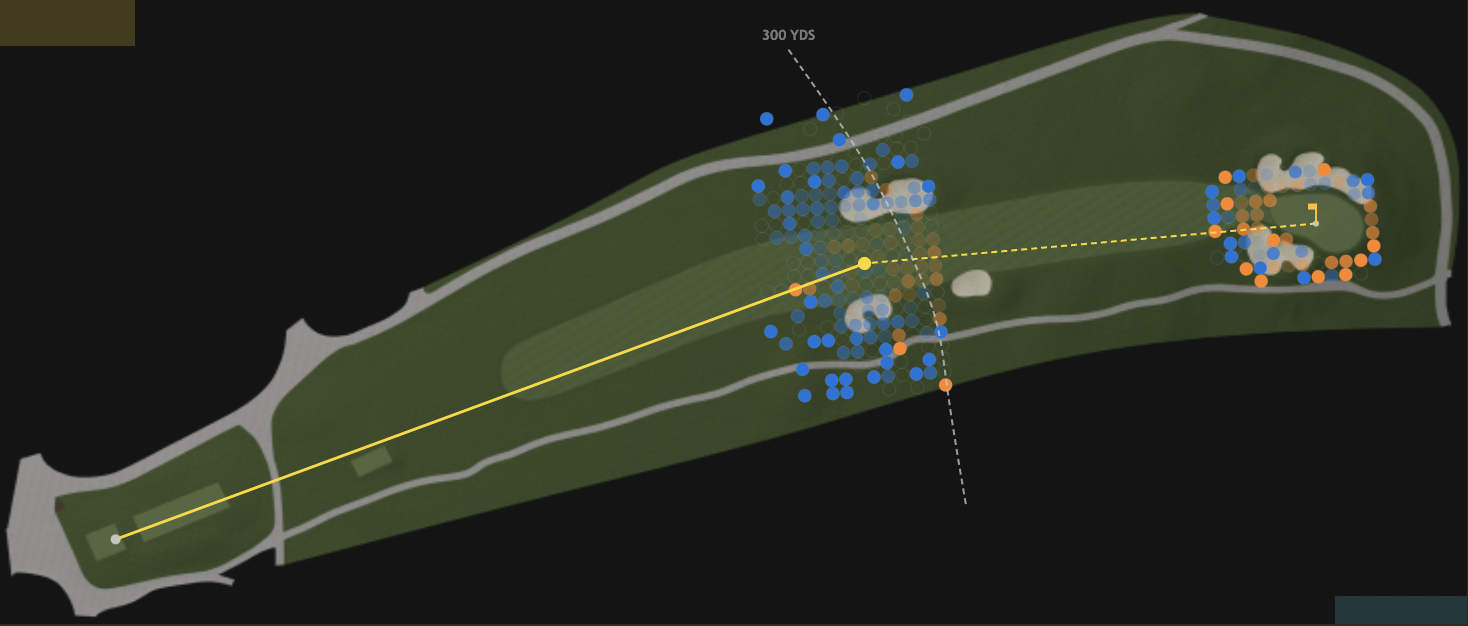
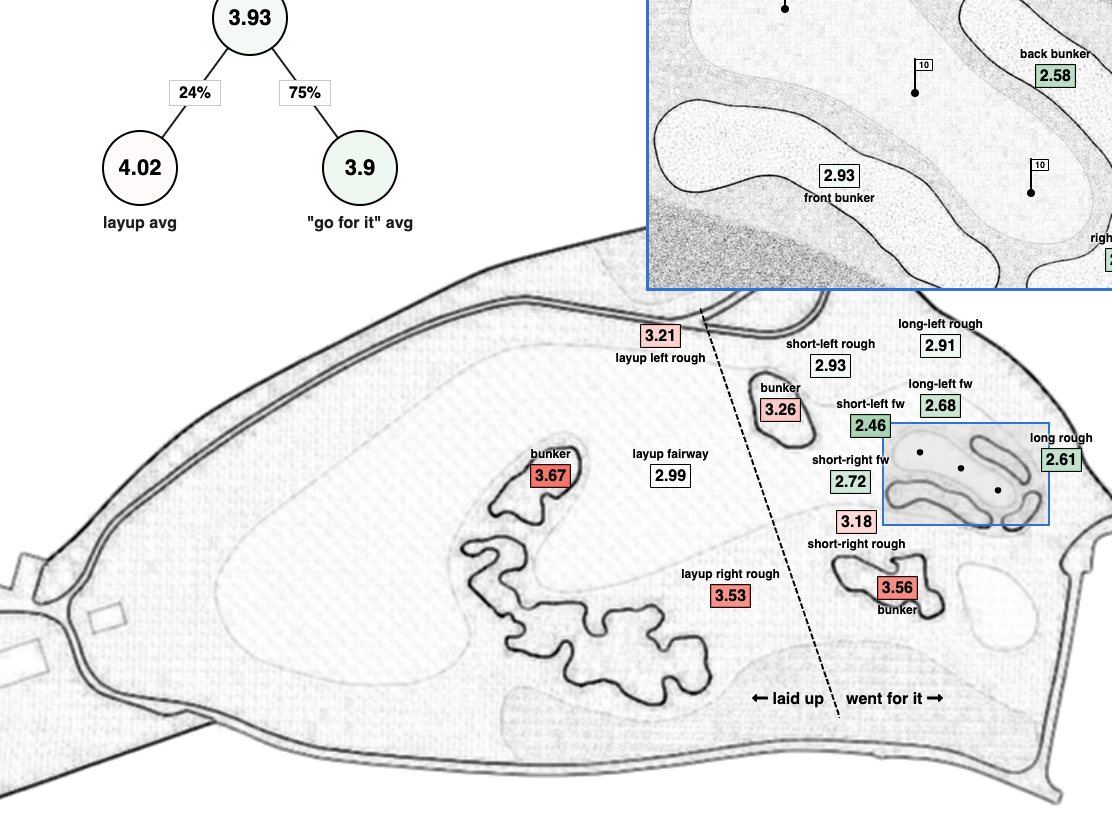
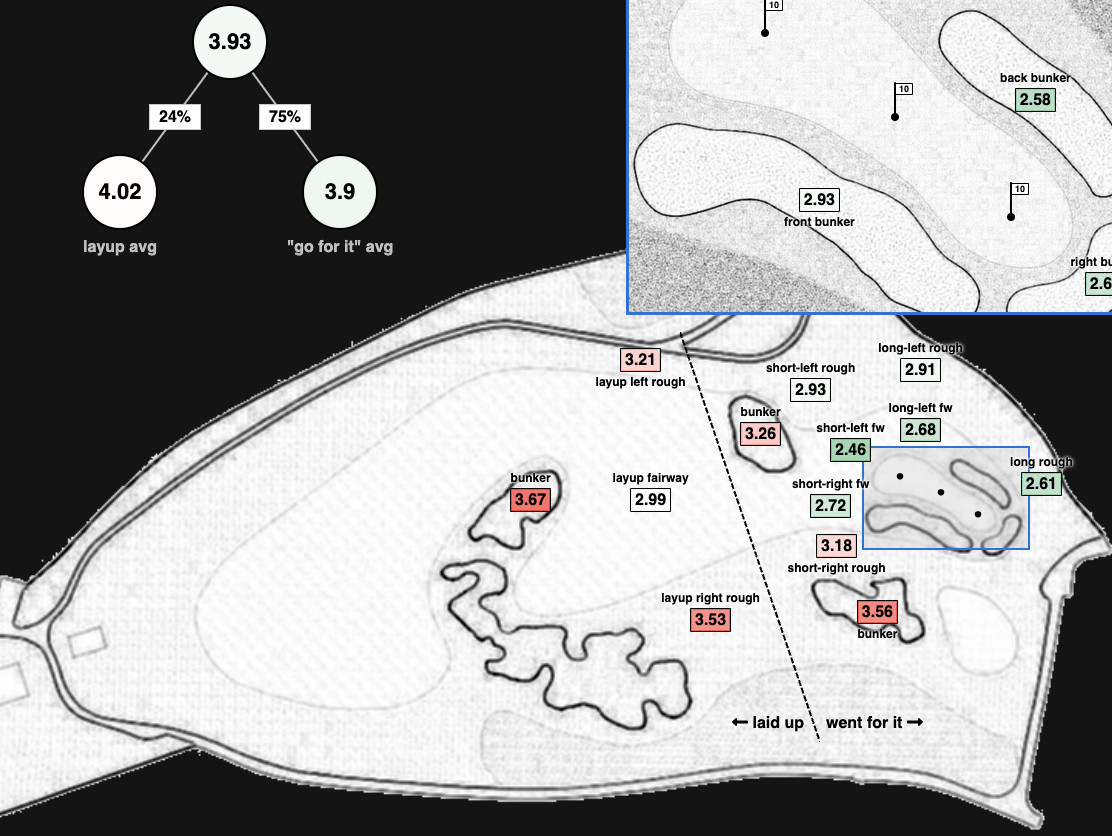
Hole Mappings
Shot-level heatmaps of every hole at Torrey Pines South.
RANKINGS
ARCHIVES
Raw Scores, Stats, and Strokes Gained
Betting Odds
DFS Points & Salaries
Betting Results
INTERACTIVES
Trend Table 



Interactive table highlighting recent performance trends around the world of golf.
Approach Skill
Using strokes-gained, proximity, and GIR to break down approach skill across 6 yardage buckets.


Historical EventTournament Stats


Comprehensive statistical breakdown of past PGA Tour tournaments.
Course Fit Tool
Are certain skill sets — such as distance, or accuracy — favoured at specific courses?


SGStrokes-Gained Distributions


Ranking and visualizing the round-level distribution of strokes-gained.
Performance Table
Pressure Tool
Who plays best (and worst!) under pressure?
Career Projections



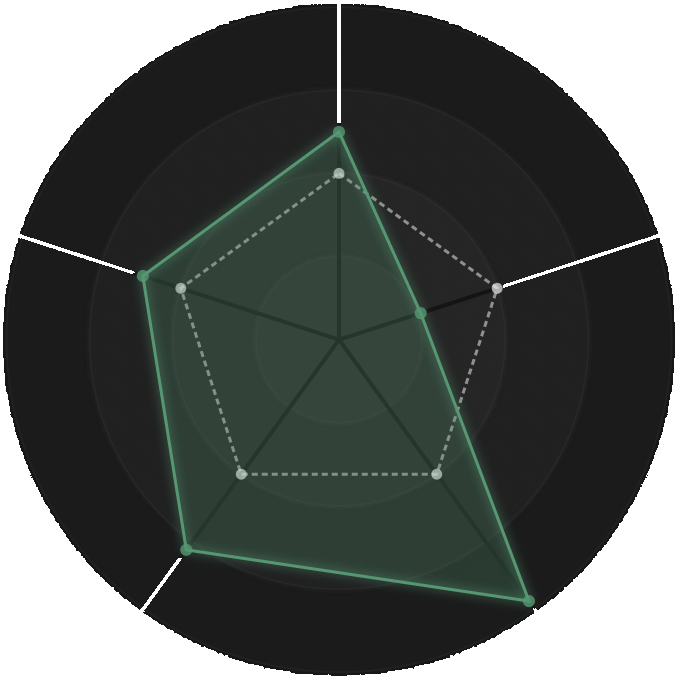
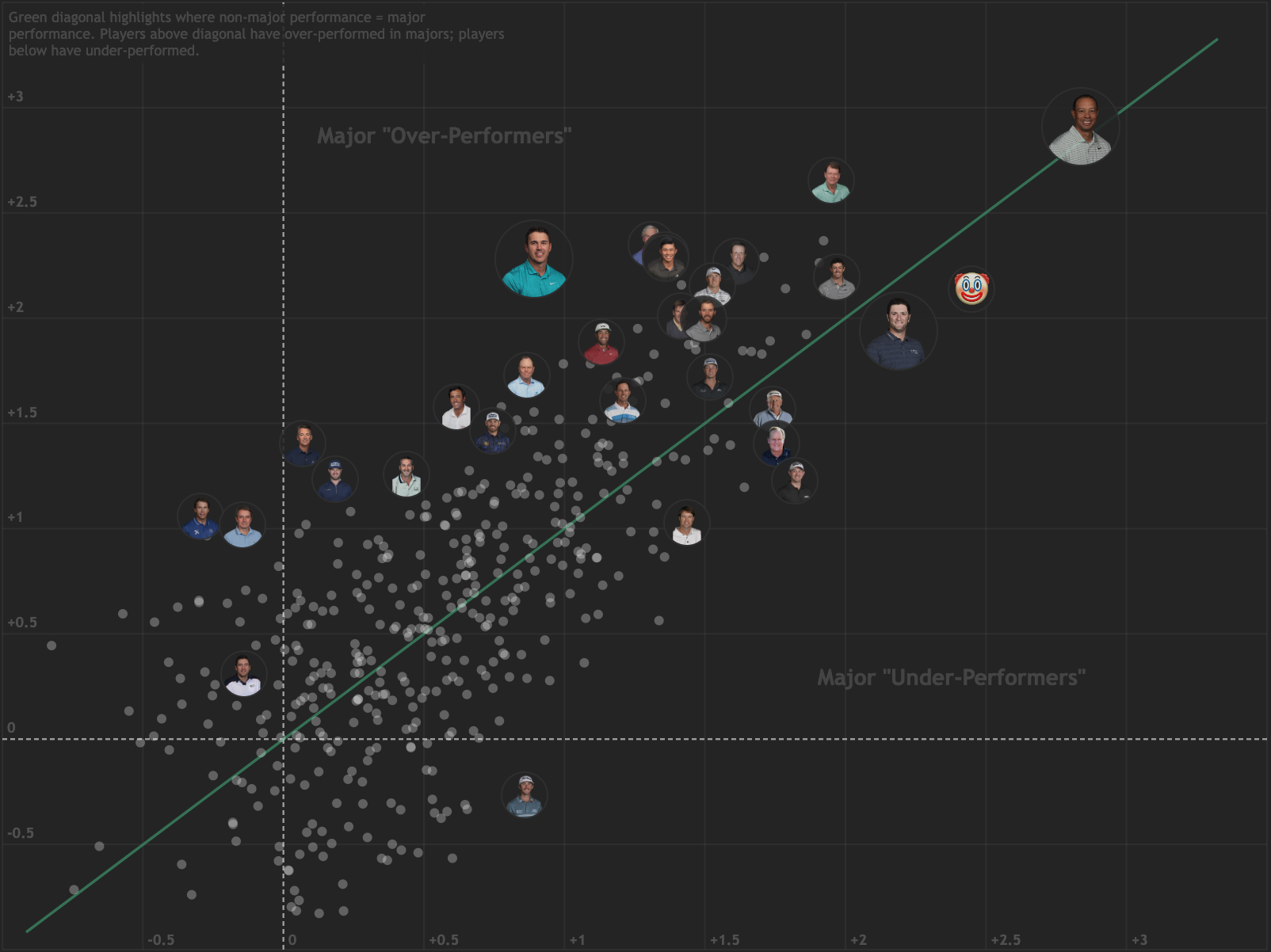
 Major Championship Data Visualizations
Major Championship Data Visualizations
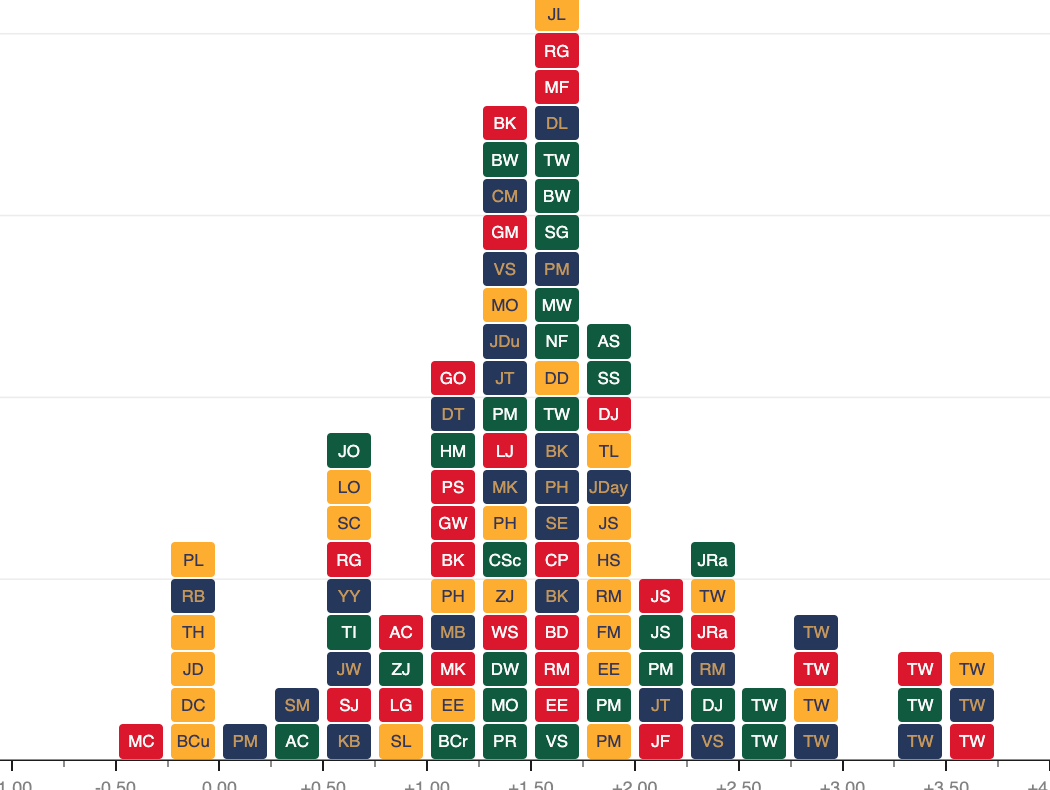
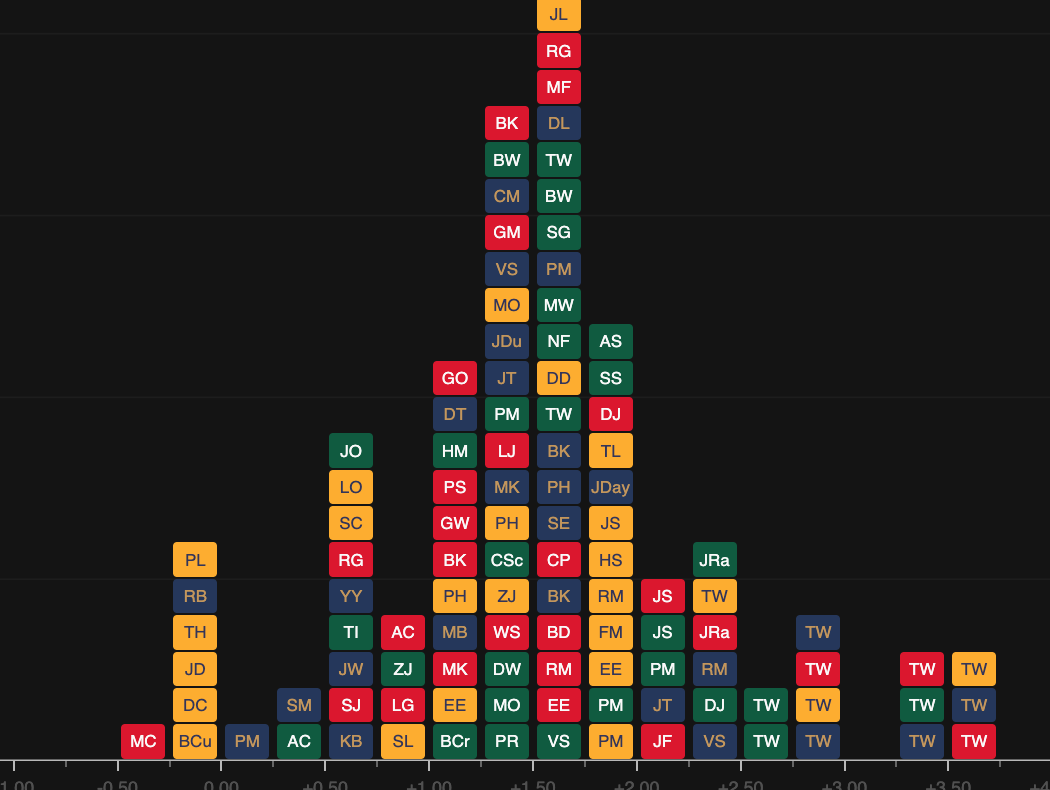
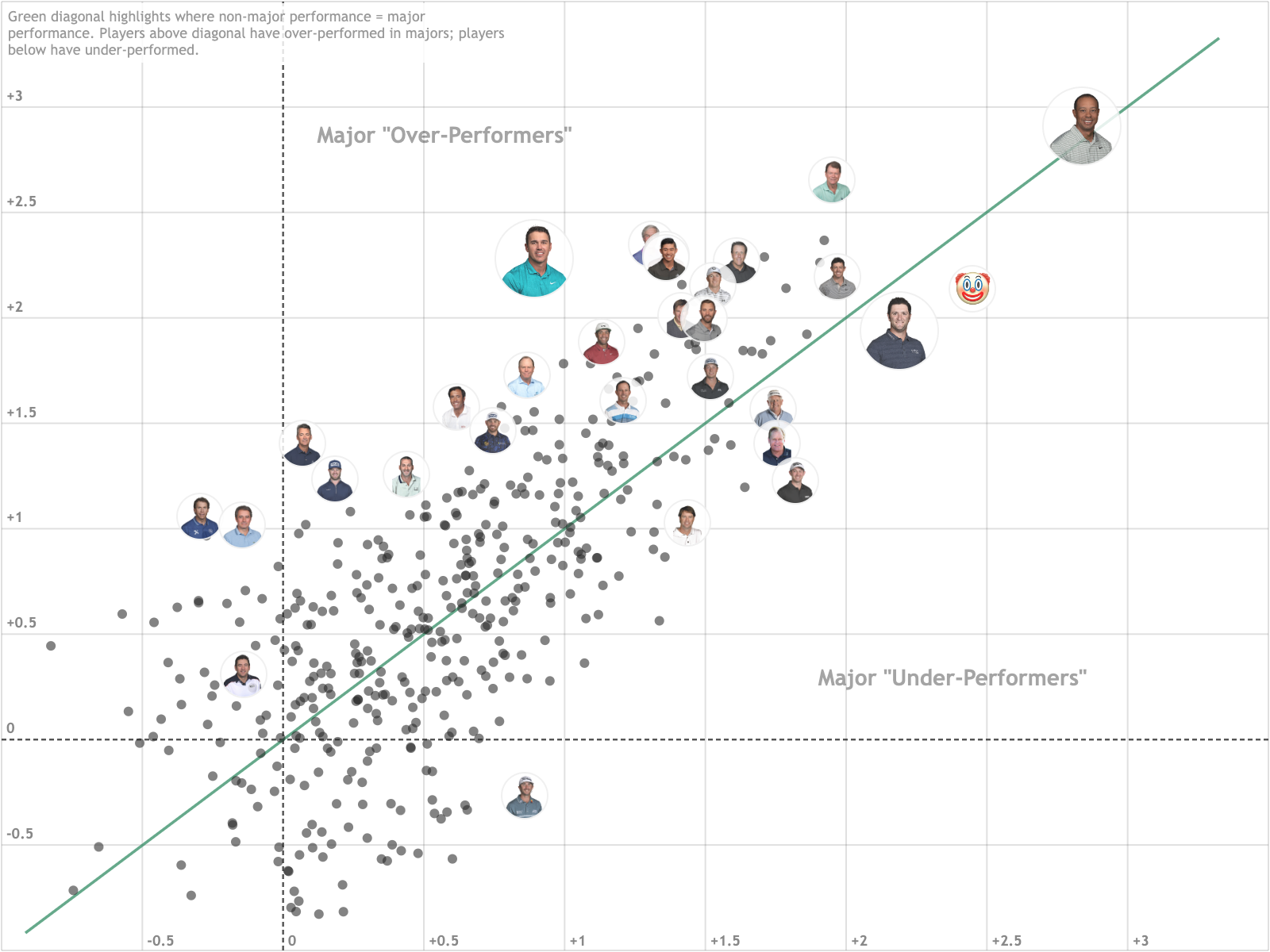

 S. SCHEFFLER
S. SCHEFFLER L. ABERG
L. ABERG R. MCILROY
R. MCILROY J. RAHM
J. RAHM D. WENYI
D. WENYI A. CHESTERS
A. CHESTERS S. KIM
S. KIM
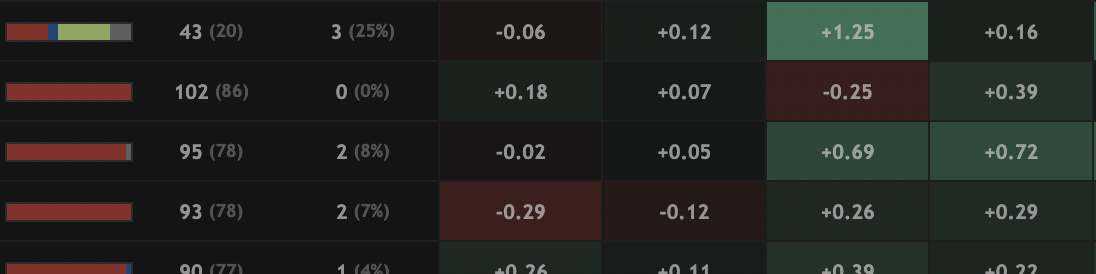
 LOWRY
LOWRY





